The team of scientists from the Research Centre "Fundamental Problems of Thermophysics and Mechanics" of Samara Polytech offers new ways to improve the performance, strength and reliability of machines for various purposes and their elements. Through the use of the basis of new methods for predicting, calculating and modeling locally nonequilibrium processes of dynamic thermoelasticity, oscillations and self-oscillations, taking into account the relaxation properties of materials.
During the process of testing, debugging and operating spacecraft, emergency situations of the behavior of systems and assemblies are revealed. The analysis of emergency situations shows the presence of previously unpredicted (not taken into account) factors of influence. This is due to the fact that engineering techniques and general design methodologies do not take into account the local nonequilibrium of the processes of heat, mass and momentum transfer, which leads to significant errors in their description by standard local equilibrium models.
«The development of methods that predict the behavior of machine elements in standard and abnormal (extreme) operating conditions is a strategically urgent task, the solution of which will provide a given (predictable) resource, high reliability, performance, and, consequently, the competitiveness of domestic developments in the aerospace industry», - explains Director of the Research Center "Fundamental Problems of Thermophysics and Mechanics", Ph.D. Professor I.V. Kudinov..
In order to create new experimental-theoretical models of vibrational processes of elastic bodies, experimental studies of longitudinal vibrations of rod structures were carried out on the basis of the testing laboratory of the Space Rocket Centre Progress. Experimental and theoretical research made it possible to clarify the mathematical models of the vibration processes of elastic bodies by determining the relaxation coefficients and, thereby, to bring the mathematical models as close as possible to the description of real physical processes. Taking relaxation phenomena into account made it possible to reduce the error of the theoretical model in comparison with experimental data from 42% to 15% (Fig. 1). Such verification of the model when using software systems that implement it made it possible to abandon a number of expensive experimental studies carried out in the process of ground testing of rocket and space technology.
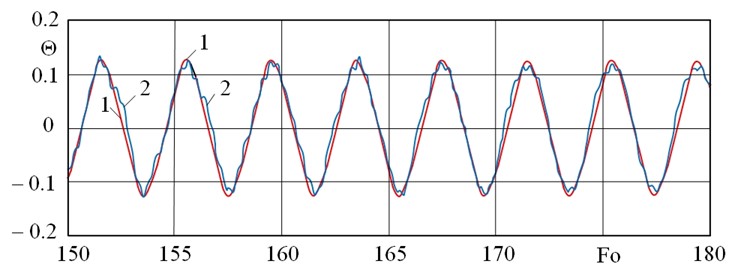
Fig.1. Rod oscillations at the sections of linear amplitude change (scaled-up); 1 – calculation based on the modified Hooke's law; 2 – experiment in the time range. Θ, Fo – dimensionless motion and time.
The obtained results can be used to calculate rod structures subject to instantaneous impact forces and alternating cyclic loads. The most important theoretical and practical result from the study is the discovery of high-frequency, low-amplitude oscillations observed during the rod's movement from one extreme position to another. It was discovered by accounting for the relaxation properties of the materials. These oscillations cause a high-frequency oscillation process throughout the entire structure due to the accumulation of low-cycle fatigue, which diminishes the margin of safety of the material. Knowledge of the physical mechanism behind such oscillation processes allows us to develop a set of measures designed to minimize its impact on the structures' performance. Specifically, these measures would aim at eliminating the resonance oscillations and beating, which are determined by comparing the natural and forced oscillations.
For reference
The work is carried out within the framework of the project "Mathematical Models for Oscillating Processes, Heat and Mass Transfer and Thermomechanics with Dual-Phase and Multiphase Lagging - Development, Theoretical Research, and Experimental Verification" This project was among the winners of the Russian Foundation for Basic Research “Stability”
