A unique approach to designing robust, calculation-based online assessments

My area of teaching involves students learning how to analyse, interpret and solve calculation-based practical problems based on physics, optics and mathematics. One of my biggest challenges in recent years has been designing open-book, online assessments (both formative and summative) that use calculation-based problems, but remain robust against cheating, particularly through student collusion.

Designing a valid methodology

After discussing concerns with colleagues, researching and deliberating on an assortment of methods that have been used to prevent collusion in open-book assessments, I concluded that four realistic and deliverable approaches should be used, conjointly:

• preventing backtracking to any previously answered questions,
• randomisation of the order of presentation of the questions,
• setting a defined expiry time, beyond which the assessment automatically gets cut off and submitted,
• setting a defined assessment “window” period, beyond which the assessment cannot be started nor submitted.

I opted to use my university’s virtual learning environment (VLE), Blackboard, for delivering my assessments, because it enabled all four approaches simultaneously. Other VLEs will probably allow the same actions.

A formula-based question approach

I used a formula-based question function to create calculation-based problems that used individual variables instead of discrete numbers. Figure 1 is an example of a question containing such variables.

Image

I could then encode the physics-based equation that solves the problem set within the formula-based question – see Figure 2.

Image

The formula-based question function specifies important options for the answer that can be selected to illustrate how learners must present their answers, for example, the number of required decimal places. It also defines how many different answer sets should be created for different versions of the question.

So, each formula-based question can be repeated several times with different variable values generating a range of questions that are put to students, each with their own corresponding calculated answers, as per Figure 3.

Image

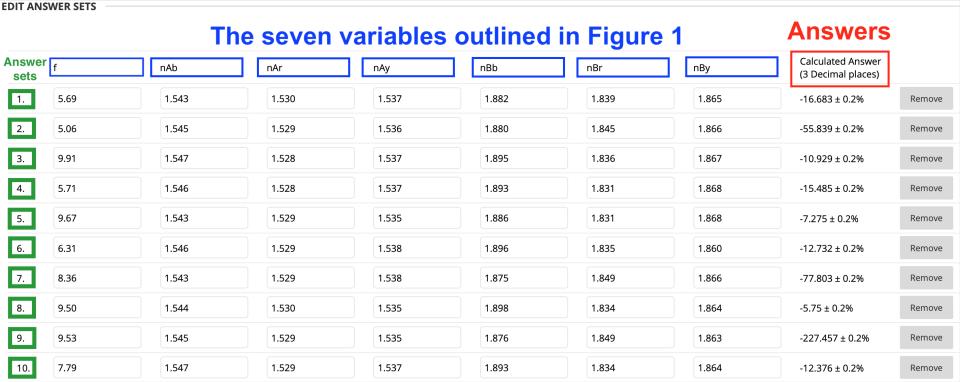
Although Figure 3 shows 10 “answer sets”, any required number can be programmed. To ensure each student sees a different version of the question from their peers, minimising the chances of collusion, I recommend setting the number of answer sets for each formula-based question to match the total number of students taking the assessment.

Each student will be presented with questions leading to completely different answers using different calculation values for each variable, but each version of the question will still assess the same intended learning outcomes. Randomisation of the order of the questions within the assessment means students will be tackling different questions at different stages of their assessment.

Additional settings to further minimise collusion include:

• a timer, limiting how long students have to complete the assessment once they start it. When this time period has passed, the assessment will be automatically submitted,
• a completion window – for instance, the test can only be started by learners within the predefined 48-hour window,
• randomising the order of appearance of the assessment’s questions,
• presenting one question at a time only, and
• prohibiting students backtracking to previously answered questions.

All five options collectively combine to reduce the risk of collusion.

This approach has received positive feedback from external examiners.

“I thought your approach to online assessments, and in particular how you managed to safeguard against collusion, was novel and inspired. I like the idea of providing different questions for each student,” wrote Gunter Loffler of Glasgow Caledonian University.

“This is a fantastic concept…it is very innovative and I don’t recall having seen anything like it before. I do agree that this approach will remove any prospect of academic misconduct,” added Kirsten Hamilton-Maxwell of Cardiff University.

Amit Navin Jinabhai is senior lecturer in optometry at the University of Manchester.

If you found this interesting and want advice and insight from academics and university staff delivered direct to your inbox each week, sign up for the THE Campus newsletter.